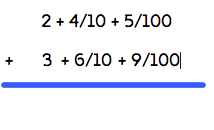Mercredi dernier, tous les enseignants de l’école la Tramontane se retrouvaient pour une journée studieuse autour de leur chef d’établissement, Philippe Béguin et de la formatrice, Françoise Duquesne. Au programme, manipuler en maths pour construire le sens du nombre. Comme me l’a expliqué Philippe, l’équipe, lors d’une concertation pédagogique de début d’année, a fait “remonter” ce besoin commun. Marion, enseignante spécialisée, a aussitôt pensé à sa formatrice connue lors de son parcours de formation… Rendez-vous a été pris…

Françoise Duquesne entre directement dans le vif du sujet en questionnant l’assistance. Très vite, on perçoit que la manipulation et les jeux de mathématiques sont utilisés largement en maternelle et en CP/CE1, un peu moins par la suite.

Jouer, manipuler ne serait-il réservé qu’aux “petits” ? Qu’aux “novices” ? Pour lancer la réflexion et amorcer la déstabilisation nécessaire à tout apprentissage, Françoise Duquesne questionne : “Comment rendre accessible des notions abstraites afin qu’elles soient construites avec du sens. S’agit-il de rendre les élèves performants ou compétents ?”  Et de rajouter : ” Le langage mathématique n’est pas une traduction mot à mot : c’est une traduction dans un autre système. Ce qu’on va traduire, c’est le sens. Dès le début des apprentissages, on n’écrit pas ce que l’on entend, il va falloir mener et accompagner un travail d’interprétation, de sens. Ce sont deux systèmes de signifiants qui n’ont pas les mêmes règles. Ceci va se retrouver à tous les niveaux de la scolarité.

Par exemple, la traduction du nombre d’après, c’est comprendre la quantité qui augmente et la suite qui continue, ou encore le concept en lui-même de l’addition est une augmentation de la quantité. C’est une traduction du concept en signifiant mathématiques. Et concernant la construction “du 10”, faire des paquets, cela demande conceptuellement de changer d’unité (passer de 10 unités discrètes, des unités séparées, à 1, une dizaine), sont mobilisés flexibilité et changement de point de vue.”(fonctions exécutives, présentes dans la zone pré-frontale).

➡ FONCTIONS EXECUTIVES le chef d’orchestre du cerveau.

L’objet de réflexion n’était pas la résolution de problème, néanmoins, c’est une préoccupation des enseignants, aussi ! Françoise rappellera des principes de base qu’il est bon de ré-entendre :

  • Qu’attend-on d’un élève qui résout un problème ?
  • Quel est l’enjeu ?
  • Est-ce du fictif ? du faux ? Il s’agira pour l’enseignant d’oraliser ce contrat. En maternelle, il est important de placer les élèves en “vraie situation”, des situations de la vie de classe afin de les mobiliser et les impliquer en leur montrant que ça va leur servir. Pourquoi a-t-on besoin du nombre ? C’est ça que l’on va mettre en musique pédagogiquement.
  • Toutes les notions du programme n’ont pas le même “poids”.
  • Les notions mathématiques ont un sens, une raison d’être.
  • Ce qui va provoquer la motivation, c’est aussi le respect de la Zone Proximale de développement des élèves.
  • La manipulation, le mot est réducteur, il sous entend que l’on fait avec les mains. On peut expérimenter mentalement, pas forcément avec les mains. Et le but, ça n’est pas de faire des manipulations mais d’expérimenter, bel et bien de rendre l’abstrait accessible.

Avant de nous mettre au travail (de manipulation, bien sûr et de “cognition mathématiques”, appellation récente qui remplace l’expression “activités de logico-maths”), Françoise Duquesne fait un petit détour pour évoquer PISA et le stress des “petits français” face aux mathématiques. En regardant de plus près les résultats, on s’aperçoit, en autre, que nos élèves préfèrent ne pas répondre que de se tromper ! Oser, se lancer, se tromper, recommencer… N’est-ce pas ainsi qu’ont fait et que font encore tous nos grands scientifiques et chercheurs ?

Le moment est venu de “manipuler”. Des ilots, du matériel et différentes tâches à effectuer. Une prise de distance pour énoncer ce que cela permet de construire chez l’élève. Au travail !

Nous allons donc devoir représenter (avec le matériel numérano) des nombres, des opérations de différentes manières, et en effectuer de une ou deux façons.

 

 

On construit le nombre avec les anneaux, puis les boites à compter (pour 10), et la tour (100) dans un premier temps. C’est la quantité que l’on visualise et que l’on manipule. La possibilité de superposer les boites est intéressante, ainsi, l’élève qui veut se “rassurer” sur la quantité comptée (on ne sait jamais, elle pourrait avoir disparu !! Permanence du nombre !!) n’a qu’à soulever la boite du dessus et constater que ce qu’il a dénombré est toujours là.

Nous allons tout de suite faire compter non de 1 en 1 mais de 10 en 10… eh oui, ça surprend, mais rappelez-vous, faire des maths demande flexibilité et non rigidité !!

Nous allons ensuite positionner ces anneaux sur les abaques. En commençant par la droite. C’est la visualisation de la position et son importance que l’on réalise là. On peut mettre des étiquettes anneaux, boite, tour, sous chaque abaque.

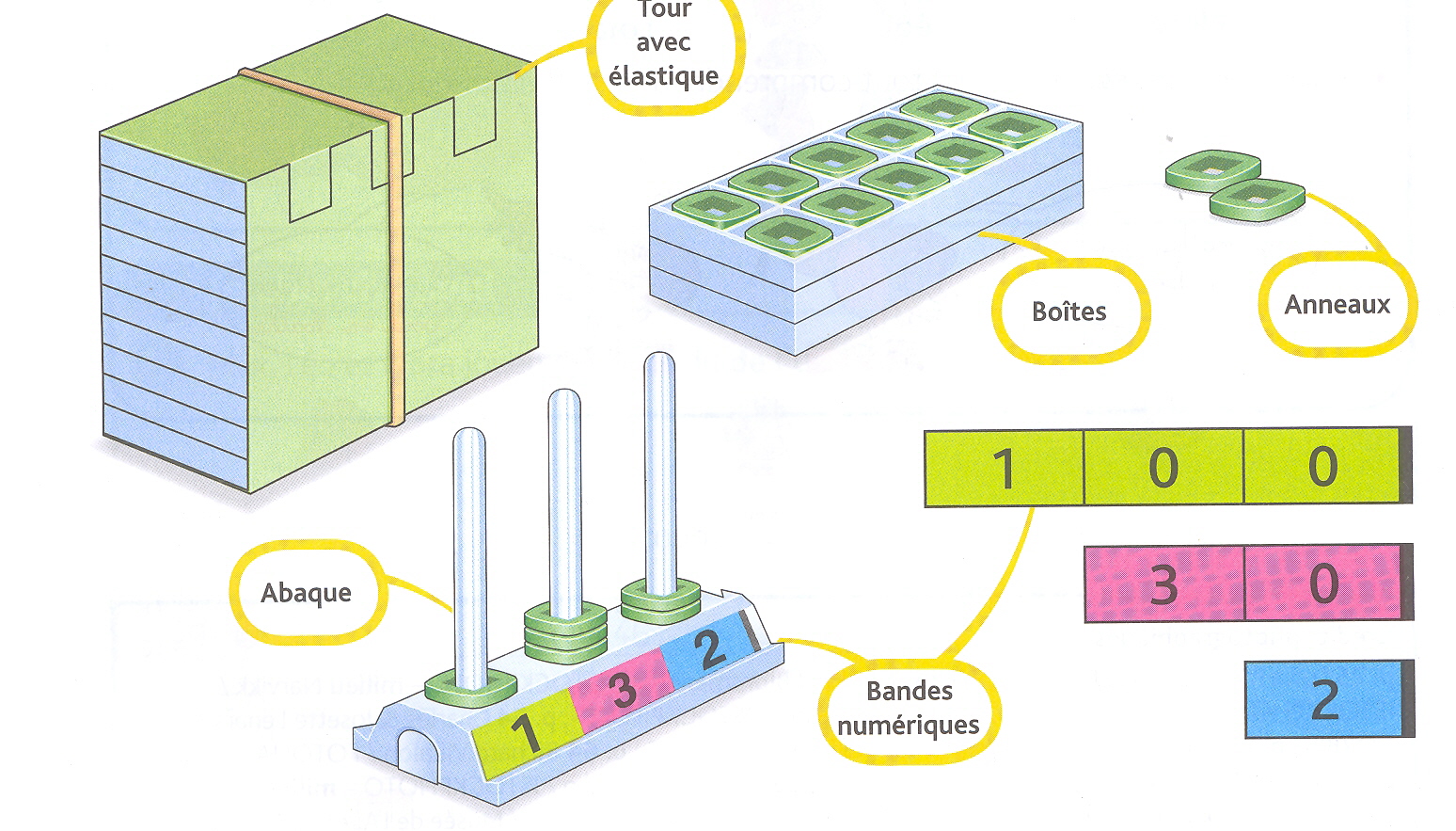On va ensuite passer au transcodage, et utiliser les étiquettes nombres et visualiser l’écriture, par exemple : 100 + 30 + 2 pour en arriver à l’écriture qui prend en compte la position : 132

Avec plus ou moins de dextérité, nous réalisons ensuite des opérations, juste avec le matériel… Ainsi, opérer sur deux nombres permet de renforcer la compréhension de notre système de numération, et non l’inverse ! C’est le calcul au service de la compréhension de la numération. Grâce à l’utilisation des tranches de trois, visibles sur les abaques qui s’accrochent entre eux, on va pouvoir inférer la construction des millions, et des milliards.

Nous partageons nos réussites et nos questions entre groupes et Françoise stabilise tout ceci par quelques explications complémentaires : “Il est très important de montrer qu’il y a plusieurs façons d’écrire un nombre, qu’il y a différentes représentations d’un nombre. Jusqu’à la 3ème, on apprend à traduire d’une façon à une autre façon de les dire. Ensuite, on va être davantage dans la créativité. Le calcul figuré, c’est faire du calcul avec du matériel. Et c’est essentiel de manipuler. La manipulation va s’inscrire au niveau kinesthésique puis au niveau mental.”

Nous évoquons ensuite les nombres décimaux et les nombres à virgules, Françoise conseille aux collègues de cycle 3 de laisser longtemps l’écriture de ceux-ci avec l’écriture fractionnaire et ne pas passer trop vite à la virgule :

2 + 4/10 + 5/100 = 2,45, y compris pour poser des opérations :

Surprenant, non ? Intéressant aussi, comme changement de point de vue et de nécessaire flexibilité. Voir les choses sous différents angles permet de concevoir plus aisément la différenciation, j’en suis convaincue. A télécharger ci-dessous, le diaporama d’une conférence sur la différenciation et les maths, donnée par Françoise Duquesne.

➡ conference_Nathan_CDDP_val_d_oise_2011

Pour finir l’après-midi, nous explorerons différents jeux de numération que nous propose Françoise, il y en a pour tous les niveaux de classe. A vos plastifieuses !!

Vous pourrez en retrouver quelques uns ici et ici, et encore là.

 

 

 

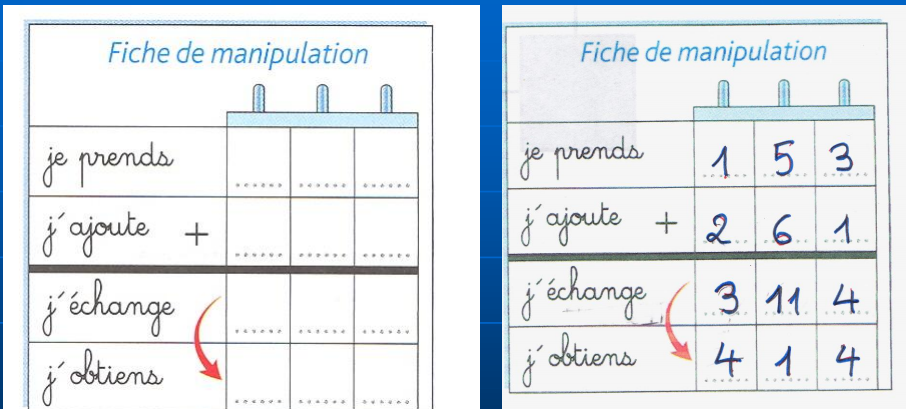
Avant de laisser Françoise nous parler d’un projet vraiment intéressant, à l’image du ROLL, mais pour les mathématiques, écoutons Amandine, enseignante ressource nous dire ce qu’elle garde de cette intervention : “Dans nos classes de CP, nous poursuivons le travail en ateliers, bien connu des maternelles, dont voici les modalités de travail : 4 groupes hétérogènes de 6 ou 7 élèves, 4 ateliers qui tournent sur les 4 jours de la semaine, 1 activité avec l’enseignante, les 3 autres fonctionnent en autonomie. C’est l’occasion de manipuler en petit groupe, réinvestir ses connaissances en jouant, s’entraîner avec divers niveaux de difficulté, apprendre de ses pairs par imitation… Suite à la journée de formation avec Françoise Duquesne, nous avons pris conscience que nous pouvions apporter quelques améliorations à nos manipulations en numération. En effet après tout le travail sur les quantités et le groupement par paquet de 10, nous procédions au travail sur les échanges de 10 u contre 1 d avec les cubes et les barres de cubes. Or pourquoi utiliser du matériel avec un visuel différent pour dizaine et unité alors qu’il n’y a aucune différence visuelle entre dizaine et unité dans un nombre écrit en chiffres. Tout est uniquement questio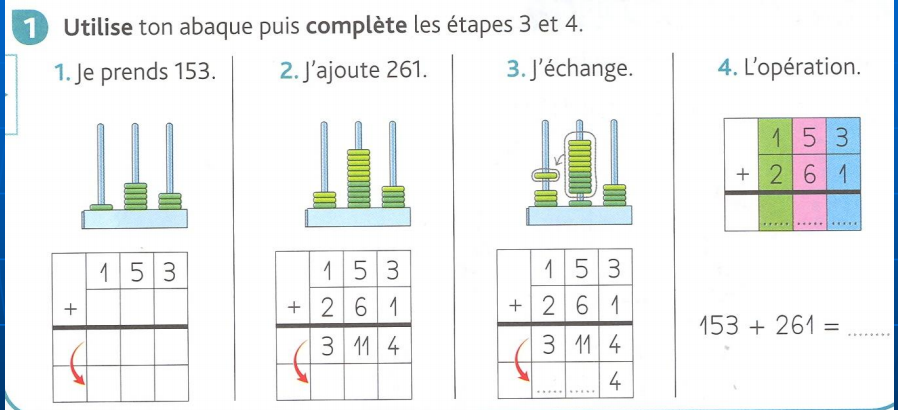n de position ! Les abaques avec des anneaux identiques sont donc une meilleure alternative pour travailler la valeur positionnelle des chiffres et les calculs le meilleur terrain de jeux pour les échanges ! Pour la technique opératoire de l’addition, certains élèves rencontrent des difficultés avec la retenue. Ils ne commencent pas par calculer les unités ou bien oublient d’écrire la retenue. Françoise Duquesne propose une ligne de calcul intermédiaire avant le résultat final. Du coup plus besoin d’imposer aux élèves de commencer par calculer les unités et plus d’oubli de la retenue puisqu’on la barre dans le résultat intermédiaire avant de la basculer dans la colonne des dizaines! C’est très efficace j ai testé avec mes élèves cette semaine !”

 

Avant de nous quitter, Françoise Duquesne nous parlera de ce beau projet qu’est “ROMA”. Pour vous, lectrices, lecteurs du blog, elle a rédigé ce texte de présentation qu’elle m’a envoyé. Souhaitons que cette “plateforme” voit vite le jour (normalement, à la rentrée prochaine). On vous tiendra au courant, promis !

“ROMA est un des dispositifs du Centre International de Formation à Distance des Maîtres (CIFODEM, centre de recherche-action à l’université Paris Descartes). Les conceptions didactique et pédagogique de ROMA sont élaborées par Françoise DUQUESNE-BELFAIS et Marie-Alix GIRODET, maitres de conférences en mathématiques. Sa conception informatique est effectuée par Michel SAVY. Ce travail est réalisé sous la direction d’Alain BENTOLILA.

L’action de ROMA vise à prévenir les difficultés des élèves dans les apprentissages mathématiques révélées par les évaluations internationales, ce plus particulièrement en résolution de problème. Le dispositif tente de développer une pédagogie de la compréhension des problèmes et de l’acte de résolution lui-même. Dans cette perspective, il accorde autant d’importance à la construction des démarches de résolution et de raisonnement qu’à l’acquisition et à l’entrainement des connaissances mathématiques attachées aux programmes.

Quelques points essentiels méritent d’être soulignés :

  1. ROMA met au centre même de sa proposition une démarche scientifique de     compréhension des problèmes et de leur résolution, démarche spécifique à l’activité mathématique.
  2. ROMA met en place des Ateliers de Compréhension de Problèmes (ACP) en groupes restreints qui permettent de favoriser les échanges entre élèves et de construire collectivement des stratégies de compréhension pour pouvoir résoudre ensuite individuellement des problèmes mathématiques.
  3. Les situations problèmes des ateliers ACP sont de trois types et alternent dans les séances :

💡 Des problèmes de type I pour apprendre à :

  • tirer des informations de différents supports : image, texte, schéma, tableau, graphique…
  • traduire des informations d’un support à un autre
  • organiser et traiter logiquement les informations

💡 Des problèmes de type II pour apprendre à :

  • reconnaitre les différentes structures additives des problèmes arithmétiques
  • reconnaitre les différentes structures multiplicatives des problèmes arithmétiques

💡 Des problèmes de type III pour apprendre à :

  • gérer simultanément la prise d’informations et leur traitement dans des tâches complexes
  • organiser un raisonnement à plusieurs étapes

Enfin, les trois types de problèmes permettent d’apprendre à justifier et communiquer une résolution.

  1. En parallèle aux Ateliers de Compréhension de Problèmes, ROMA permet d’organiser des parcours de travail différenciés sur chacune des compétences du programme d’un niveau de classe au cours des Activités d’Entrainement Individualisées (ou AEI).
  2. Les AEI de ROMA permettent à chaque élève de travailler de façon autonome et à l’enseignant de suivre individuellement leur parcours grâce à l’automatisation informatique de ROMA. Chacune des compétences du programme est évaluée à l’aide de 4 questions. L’analyse des réponses de chaque élève est effectuée automatiquement par le logiciel de ROMA. Selon le résultat obtenu par l’élève, ce dernier est orienté automatiquement vers les activités qui lui correspondent suivant un parcours différencié à trois niveaux.
  3. Comme le ROLL, ROMA est conçu pour faciliter solidarité et mutualisation entre les enseignants. Au fur et à mesure de leur développement, les observatoires locaux animés par un tuteur produiront des fiches pédagogiques et des fiches de formations en relation avec l’équipe nationale. C’est donc un réseau en constante mutation, à l’écoute de ses utilisateurs mais un réseau dans lequel la cohérence et la qualité de la démarche pédagogique sont assurées avec responsabilité par l’équipe nationale.”

💡 De nombreuses pistes, ressources pour les maths à retrouver sur “Accueillir les Différences” ici, et là et encore ici, et encore là !

➡ progression-de-cycle-3 , un exemple de progression que je trouve vraiment bien fait et qui permet le lien CM/6ème, réalisée par l’Académie de Bordeaux (vous y trouverez également des exemples de progression pour le cycle 4)

 

Géométrie de Jean-Luc Moreau

Deux droites parallèles
Depuis longtemps s’aimaient.
– Nous toucher, disaient-elles.
Le pourrons-nous jamais ?
Messieurs les géomètres
Nous parlent d’infini ;
C’est bien beau de promettre,
Mais tant de kilomètres
Ça donne le tournis !
– Si le sort vous accable,
Leur répondis-je alors,
Rapprochez-vous, que diable,
Rapprochez-vous encor !
Ma remarque opportune
Leur fut d’un grand secours :
Il n’en reste plus qu’une,
Quel beau roman d’amour!

 

L’âge du capitaine de Gustave Flaubert

Puisque tu fais de la géométrie et de la trigonométrie, je vais te donner un problème :
Un navire est en mer, il est parti de Boston chargé de coton, il jauge 200 tonneaux, il fait voile vers Le Havre, le grand mât est cassé, il y a un mousse sur le gaillard d’avant, les passagers sont au nombre de douze, le vent souffle NNE, l’horloge marque trois heures un quart d’après-midi, on est au mois de mai…
On demande l’âge du capitaine.